初級編では、半球型樹脂中での「中心付近は比較的ゆがみが弱く、次に縦横に大きく膨張し、さらに外側に近づくと縁のほうに向かってつぶれる傾向」を見ました。

【図1：半球型樹脂中のコクワガタ】

このおかしなゆがみ方について、以下のツールを使って何が起こっているのか理解しようとしてみました。

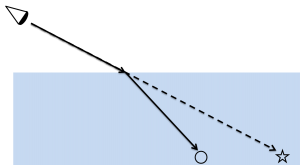
まず光の屈折の基本を確認しましょう。空気中の光が他の物質（水や樹脂など）に入射すると光の屈折が起こります。

【図2：光の屈折の基本-1】

屈折した光が眼に入ると、錯覚によって〇にあるはずのものが☆にあるように見えます（ちなみに屈折する光の軌跡は、空気中から他の物質中に光が入射するときも、逆に他の物質中から空気中に光が入射するときも同じです）。半球型樹脂でも同じことが起こっていると考えられます。

【図3：光の屈折の基本-2】

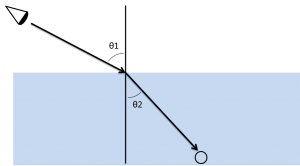
入射角θ1と屈折角θ2の関係は「スネルの法則」

sinθ1/sinθ2=n

という物理法則に従います。

nは物質ごとに決まっている値で、屈折率といいます。半球型樹脂に使ったエポキシ樹脂の屈折率は1.55-1.61で、今回は1.60とします。

半球型樹脂で光の屈折がどのように起こるのかを作図するため、KSEGというフリーの描画ソフトを使いました。KSEGは直線や円の描画から、距離や角度の測定まで簡単に操作ができる便利なソフトです。

KSEGを使って、光の通り道を1つ作図したのが以下の図です。

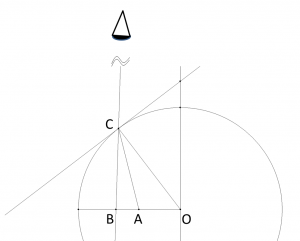
【図4：光の屈折の作図例】

Aにあった点がCで屈折して目に届きますが、実際には錯覚によってBに見えます。

ここで半球の中心の位置を0、外の縁の位置を100とします。複数の点について図4の作図を行い、点AとBの位置の関係をプロットしたのが以下の図です。

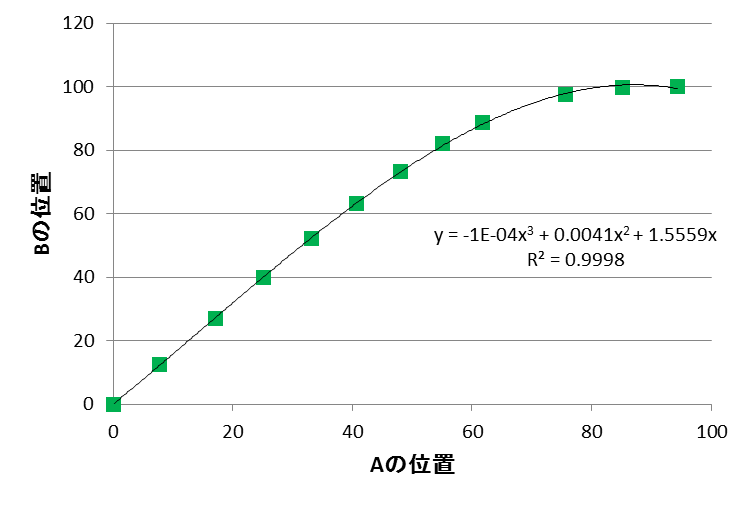
【図5：中心からAまでの距離とBまでの距離】

 また、中心からAまでの距離とBまでの距離の差（つまりどれだけ膨張するか）をプロットしたのが以下です。

【図6：中心からAまでの距離とBまでの距離の差】

60ぐらいの位置で最も膨張が激しいことがわかります。

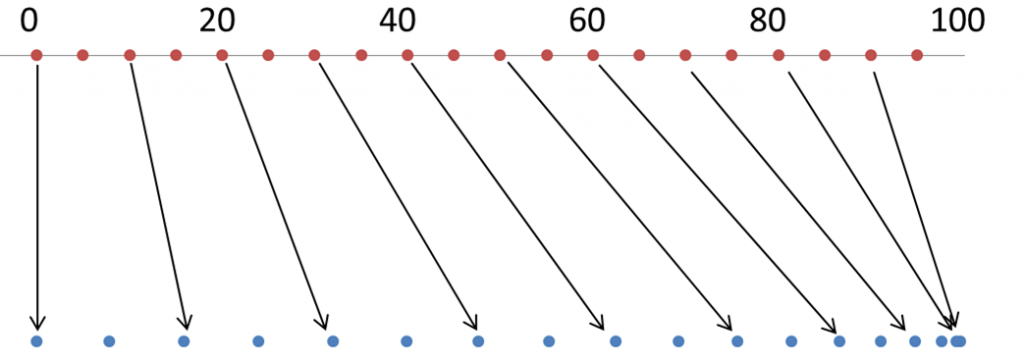
【図7：Aの位置に対するBの位置】

図7に従って、クワガタの画像をマニュアルで加工（分割した画像を図7のゆがみにしたがって引き伸ばしたのち結合） してみました。

「中心付近は比較的ゆがみが弱く、次に縦横に大きく膨張し、さらに外側に近づくと縁のほうに向かってつぶれる傾向」が再現できました。図5から図7でのモデルは、ある程度正しそうです。

図7を使うことで、ある標本を半球型樹脂に埋めたときにどう見えるか、実際に作る前に知ることができます。

結論は第一部と変わりませんが、ゆがみの全体像をとらえることができたと考えています。